
This also applies to cable, chain, and webbing.
Gear that is anchored includes anchors, rocks, trees, tripods, trucks, etc.
A "bight" is a simple loop in a rope that does not cross itself.
A "bend" is a knot that joins two ropes together. Bends can only be attached to the end of a rope.
A "hitch" is a type of knot that must be tied around another object.
"Descending devices" (e.g., ATCs, Brake Bar Racks, Figure 8s, Rescue 8s, etc) create friction as their primary purpose. The friction in descending devices is always considered when calculating forces.
The "Safety Factor" is the ratio between the gear's breaking strength and the maximum load applied to the gear (e.g., 5:1).
When calculating forces, vRigger can include, or ignore, the horizontal forces that are generated by rope angles. You enable the calculation of these "horizontal" forces by selecting the Consider Angles checkbox in the Calculations group on the Forces toolbar.
You can also display the angles between ropes.
The following three figures all show a 100-pound load hanging from an anchor.
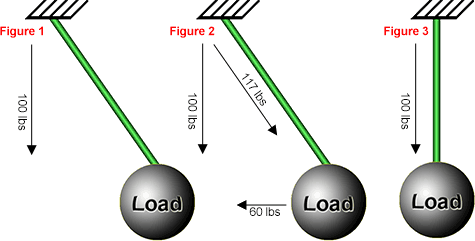
Only vertical forces were calculated in Figure 1, so the rope and anchor are each holding 100 pounds. However, in the real world, there is also a horizontal force of approximately 60 pounds trying to move the load to the left. When this 60 pounds of horizontal force is combined with the 100 pounds of vertical force, you end up with approximately 117 pounds of tension on the rope. This is shown in Figure 2.
If you select the Consider Angles checkbox and then calculate forces, the load will move to the left until it is centered under the anchor. At this point, there are 100 pounds of vertical force and no horizontal forces. This is shown in Figure 3.
As in the above example, vRigger will usually need to move gear horizontally when the Consider Angles checkbox is selected. You can use the Undo command to restore the gear to its original location.
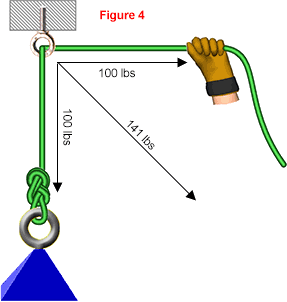
Figure 4 shows an anchor supporting a 100-pound load. If you do not calculate horizontal forces, the anchor is holding 100 pounds. However, if you consider that the load is pulling down with 100 pounds and the hand is pulling to the right with 100 pounds, the net force on the anchor is closer to 141 pounds.
The formula to calculate the net force ("NF") based on the horizontal ("H") and vertical ("V") forces is:
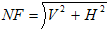
For example, Figure 4 has 100 pounds of vertical force and 100 pounds of horizontal force, so the net force is 141 pounds:
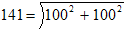
The angles in most rope systems have a relatively small impact on the forces. In Figure 4, the effect of the 90° angle increased the forces on the anchor from 100 pounds to 141 pounds which should be well within your safety factor. However, some rope systems, particularly highlines and anchors, can be overloaded due to horizontal forces.

Figure 5 shows a highline with each rope at 85° (for a total of 170°). As in the preceding systems, Figure 5 has a 100-pound load. However, due to the angle of the rope, this 100-pound load applies almost 575 pounds of force to each of the anchors. If the load was a more realistic rescue load of 500 pounds, the ropes and anchors would receive a dangerous 2,800 pounds of force.
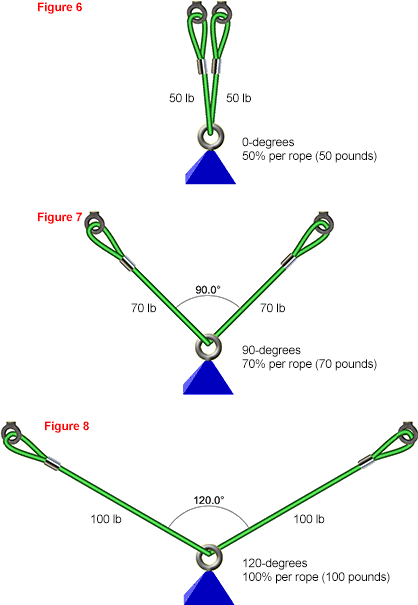
Three rules of thumb can be used to estimate the effect of angles on forces:
Many riggers limit angles to no more than 90° degrees.
Learn more about rope angle physics at RopeRescueTraining.com.